Xiaokai Zhang
PhD student, School of computer engineering and science, Shanghai University, China.
xiaokaizhang1999@163.com
     

I'm currently a first-year PhD student in the Computer Engineering and Science School at Shanghai University, supervised by Tuo Leng. Previously, I received my M.S. in computer science at Shanghai University. I am a member of SHU Geometric Cognitive Reasoning Group and the leader of FormalGeo Development Team.

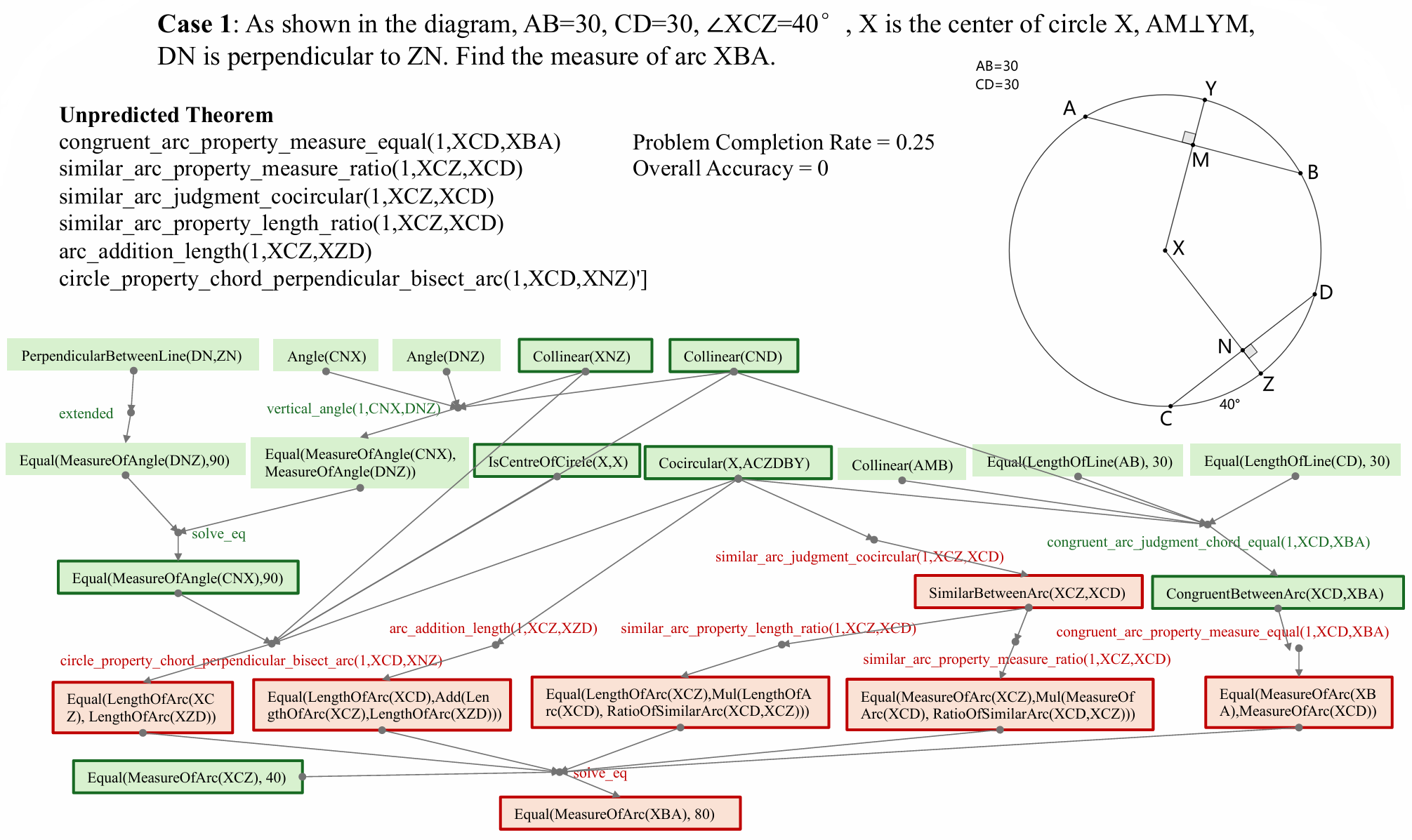
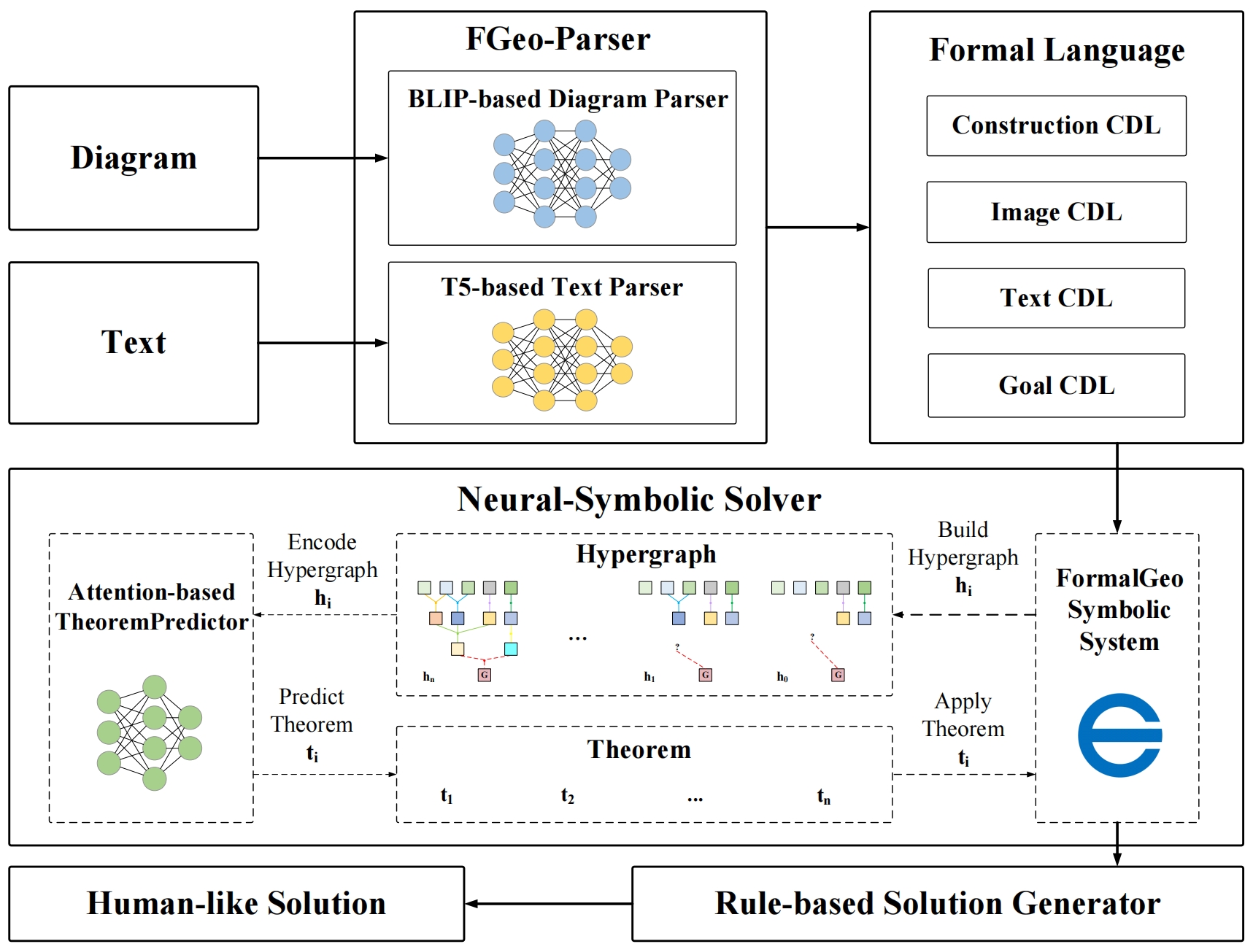
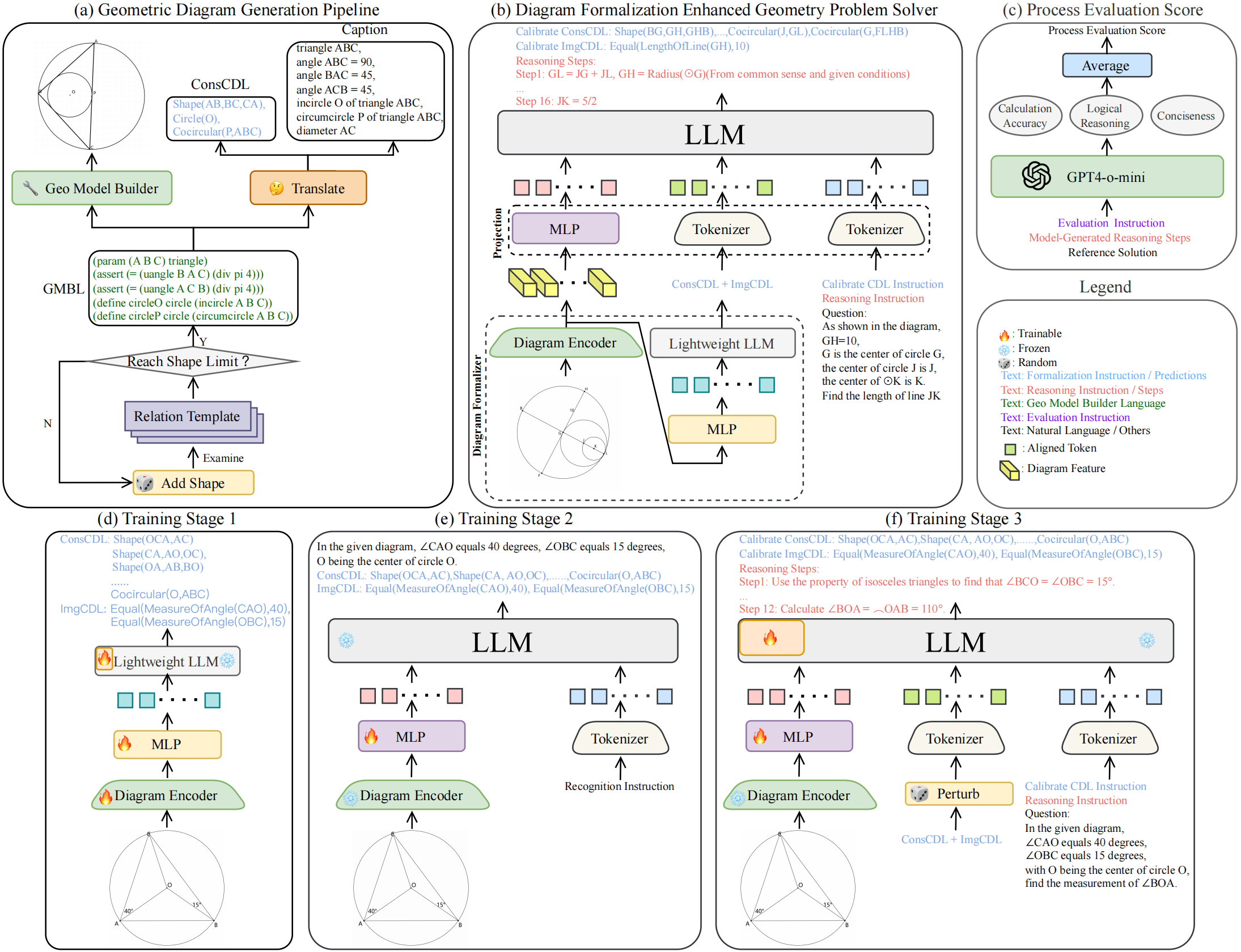
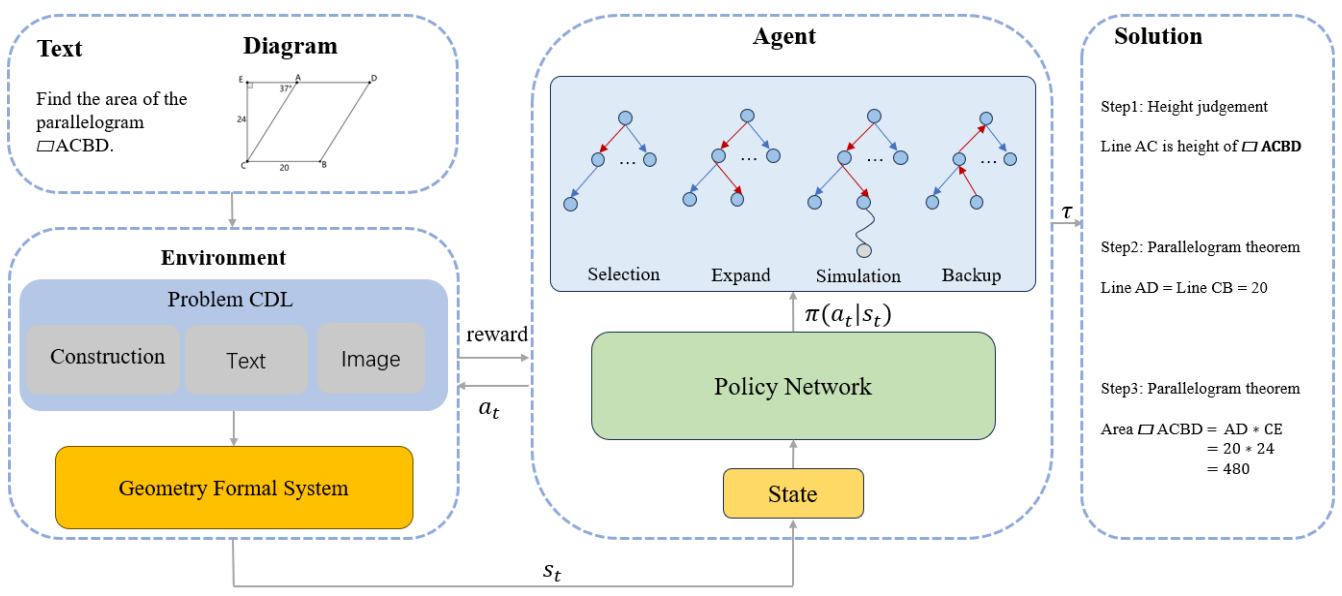
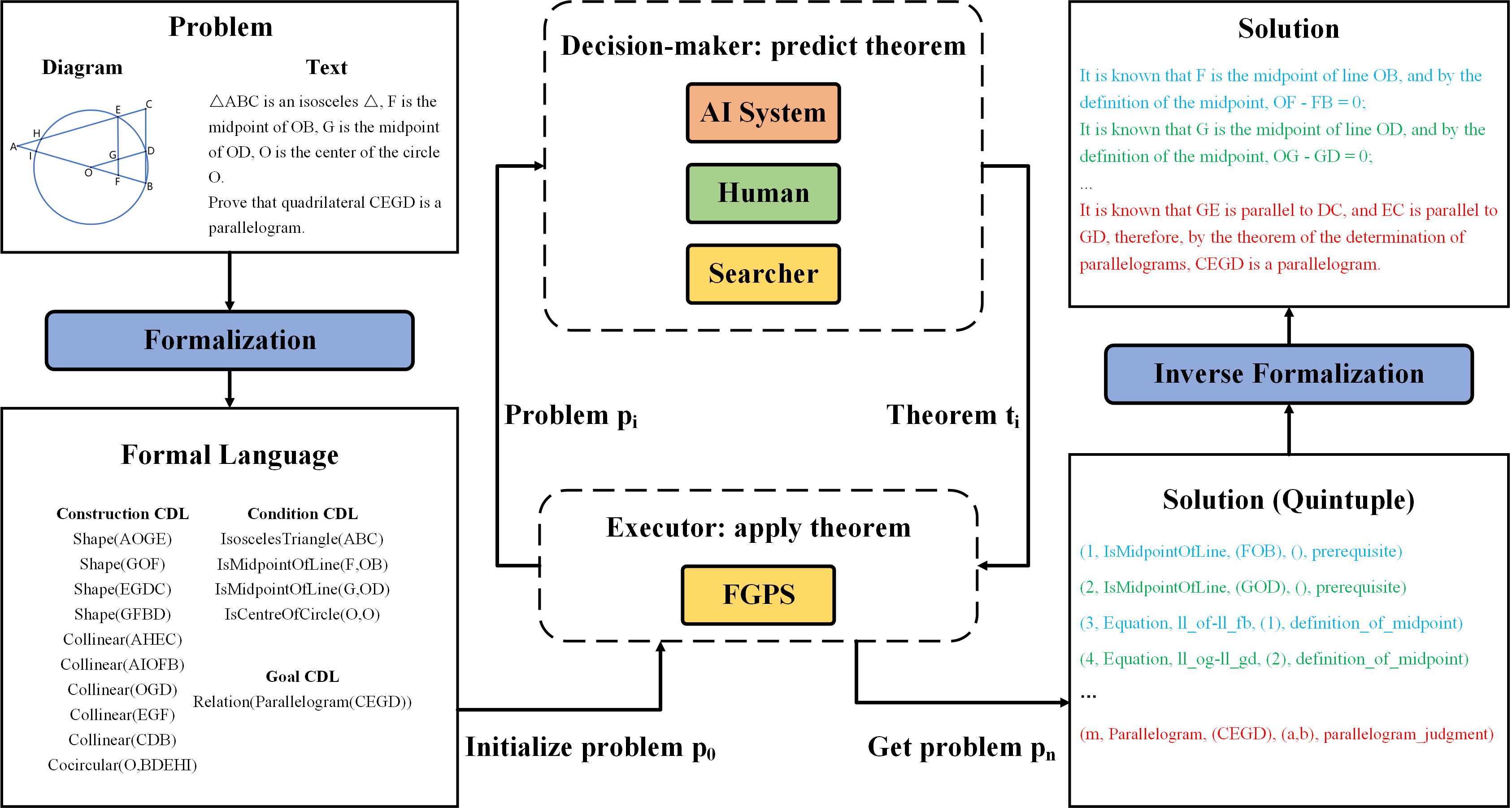
My research goal is to build an AI system to solve formalized IMO-level plane geometry problems. Specifically, the AI system can receive a formal representation of the problem, automatically solve the problem, and emit a formal (i.e. machine-checkable) proof. My primary research mainly includes the following aspects:

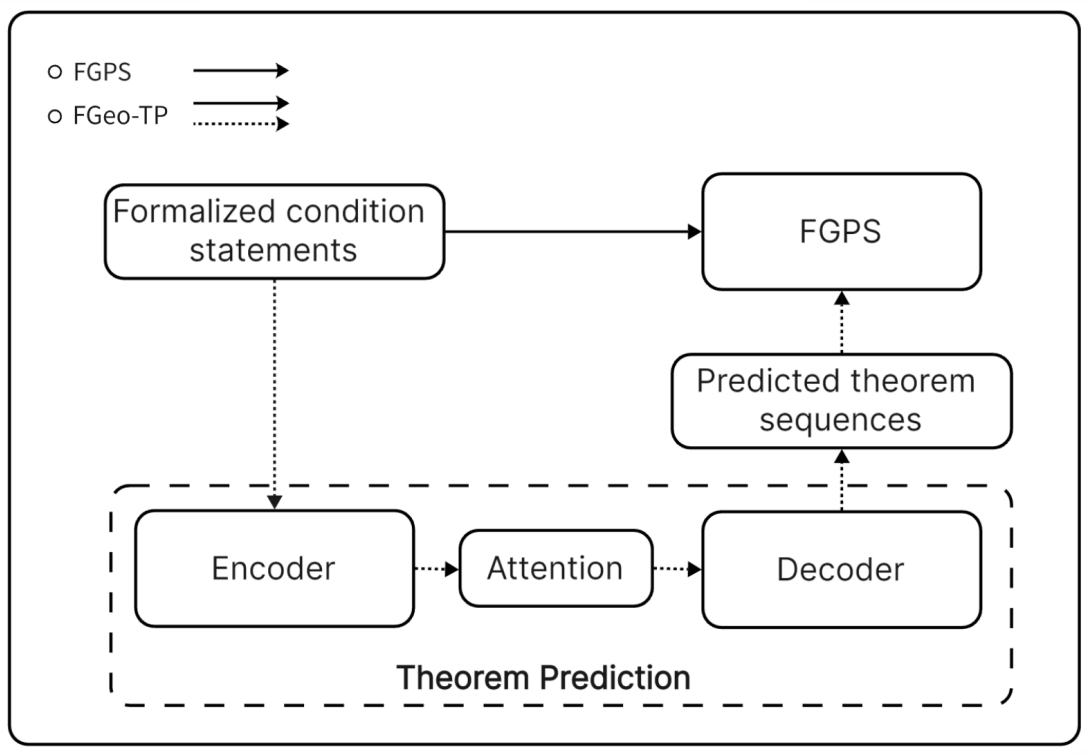
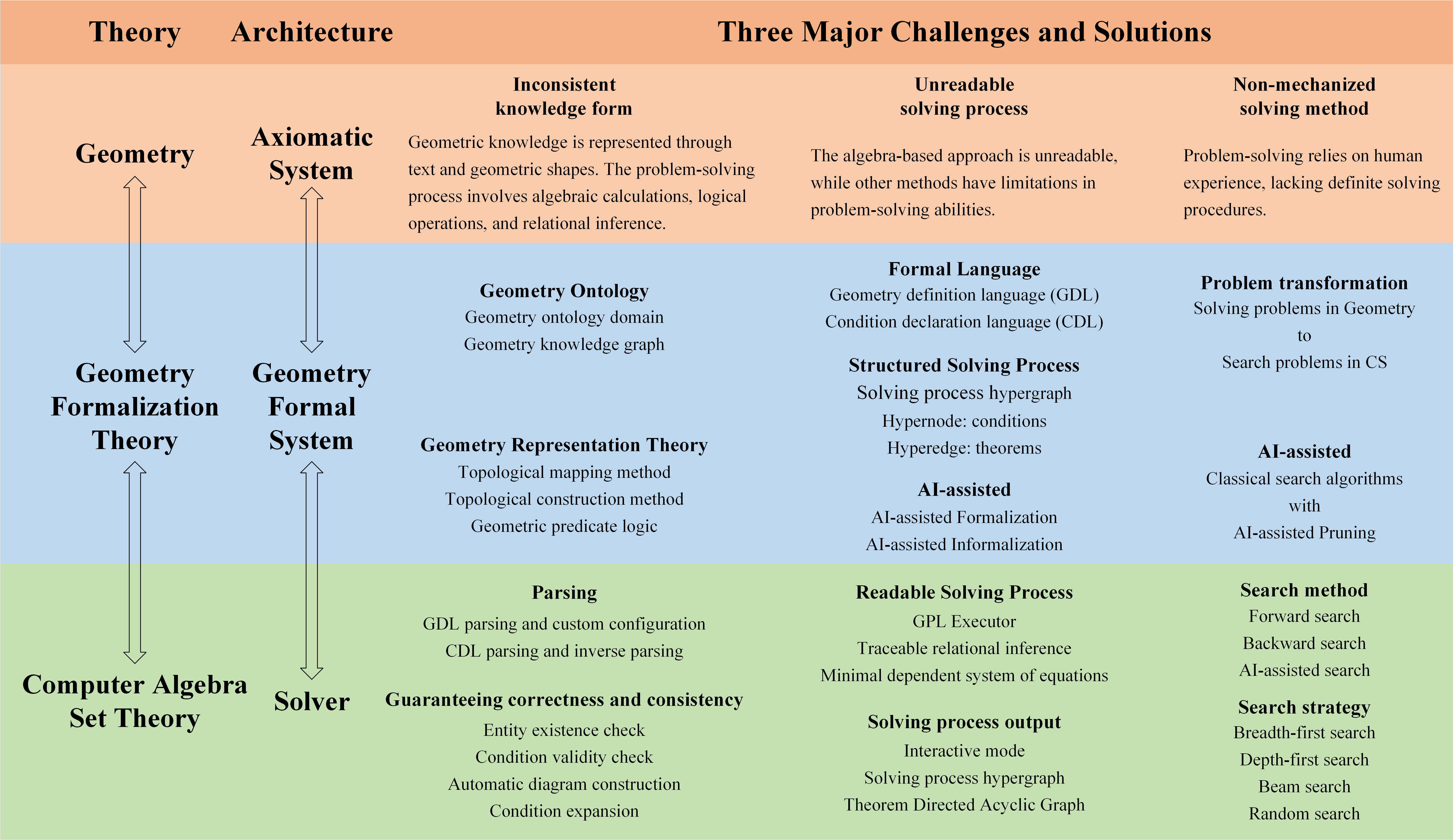
  • Formal Geometry, including geometry formalization theory, geometry formal system, formal geometric problem solver and datasets.
  • Automated Reasoning for joint solution of geometry problem combining algebraic computation and relational reasoning.
  • AI for geometry, including Autoformalization and AI-assisted problem solver.

In addition, I am interested in:

  • Reinforcement Learning for geometry problem solving.
  • Graph Neural Network for geometry knowledge embedding and geometry problem solving.
  • Multimodal reasoning for geometric problem Vision-Language automated reasoning.


News


Publications

Formal Representation and Solution of Plane Geometric Problems
Xiaokai Zhang, Na Zhu, Cheng Qin, Yang Li, Zhenbing Zeng, Tuo Leng
In this paper, we present formalgeo7k, a geometric problem dataset based on rigorous geometry formalization theory and consistent geometry formal system, serving as a benchmark for various tasks such as geometric diagram parsing and geometric problem solving.
NeurIPS 2024 Workshop on MATH-AI  [Paper]  [Project]  [BibTex]
Diagram Formalization Enhanced Multi-Modal Geometry Problem Solver
Zeren Zhang, Jo-Ku Cheng, Jingyang Deng, Lu Tian, Jinwen Ma, Ziran Qin, Xiaokai Zhang, Na Zhu, Tuo Leng
We introduce the Diagram Formalization Enhanced Geometry Problem Solver (DFE-GPS), a new framework that integrates visual features, geometric formal language, and natural language representations. We propose a novel synthetic data approach and create a large-scale geometric dataset, SynthGeo228K, annotated with both formal and natural language captions, designed to enhance the vision encoder for a better understanding of geometric structures.
arxiv: 2409.04214I  [Paper]  [Project]  [BibTex]
FGeo-HyperGNet: Geometry Problem Solving Integrating Formal Symbolic System and Hypergraph Neural Network
Xiaokai Zhang, Na Zhu, Cheng Qin, Yang Li, Zhenbing Zeng, Tuo Leng
We built a neural-symbolic system to automatically perform human-like geometric deductive reasoning. The symbolic part is a formal system built on FormalGeo and the neural part is a hypergraph neural network based on the attention mechanism.
arxiv: 2402.11461  [Paper]  [Project]  [BibTex]
FGeo-DRL:Deductive Reasoning for Geometric Problems through Deep Reinforcement Learning
Jia Zou, Xiaokai Zhang, Yiming He, Na Zhu, Tuo Leng
We built a neural-symbolic system, called FGeoDRL, to automatically perform human-like geometric deductive reasoning. The neural part is an AI agent based on reinforcement learning and the symbolic part is a reinforcement learning environment based on geometry formalization theory and FormalGeo.
Symmetry 2024  [Paper]  [Project]  [BibTex]
FGeo-TP: A Language Model-Enhanced Solver for Geometry Problems
Yiming He, Jia Zou, Xiaokai Zhang, Na Zhu, Tuo Leng
we introduced FGeo-TP (Theorem Predictor), which utilizes the language model to predict theorem sequences for solving geometry problems. Our results demonstrate a significant increase in the problem-solving success rate of the language model-enhanced FGeo-TP on the FormalGeo7k dataset, rising from 39.7% to 80.86%.
Symmetry 2024  [Paper]  [Project]  [BibTex]
FGeo-SSS: A Search-Based Symbolic Solver for Human-Like Automated Geometric Reasoning
Xiaokai Zhang, Na Zhu, Yiming He, Jia Zou, Cheng Qin, Yang Li, Tuo Leng
Based on the geometry formalization theory and the FormalGeo geometric formal system, we have developed the Formal Geometric Problem Solver (FGPS) in Python, which can serve as an interactive assistant for verifying problem-solving processes and as an automated problem solver that utilizes a variable search-based method and strategy.
Symmetry 2024  [Paper]  [Project]  [BibTex]
FormalGeo: An Extensible Formalized Framework for Olympiad Geometric Problem Solving
Xiaokai Zhang, Na Zhu, Yiming He, Jia Zou, Qike Huang, Xiaoxiao Jin, Yanjun Guo, Chenyang Mao, Zhe Zhu, Dengfeng Yue, Fangzhen Zhu, Yang Li, Yifan Wang, Yiwen Huang, Runan Wang, Cheng Qin, Zhenbing Zeng, Shaorong Xie, Xiangfeng Luo, Tuo Leng
We have constructed a complete and compatible formal plane geometry system. This will serve as a crucial bridge between IMO-level plane geometry challenges and readable AI automated reasoning. With this formal system in place, we have been able to seamlessly integrate modern AI models with our formal system.
arxiv:2310.18021  [Paper]  [Project]  [BibTex]
A method for product appearance design evaluation based on heterogeneous data
Han Lai, Zheng Wu, Xiaokai Zhang, Huchang Liao, Edmundas Kazimieras Zavadskas
This study proposes different methods to determine subjective and objective weights of criteria regarding the self-reporting, eye-tracking, and electroencephalogram data for the evaluation of product appearance design.
AEI 2023  [Paper]  [Project]  [BibTex]

Experience


Awards